Динамика роста плодовых деревьев [1976 Думбляускас А.М.

Для установления роста и развития плодовых деревьев необходимо тщательно изучить надземную часть (прирост диаметра ствола, побегов, площадь листа), которая также имеет тесную связь с подземной частью. На наших опытных участках изучали в основном сорта антоновки, которые считаются самыми распространенными в республике. На I опытном участке было 387, а на II участке - 180 деревьев.

Площадь листа определяли при каждом варианте осушения. С этой целью выделяли 3-5 типичных здоровых дерева, с которых срывали 100 листьев. После их взвешивания вычисляли площадь листовых пластинок по методике М. К. Полякова. Для этого измеряли наибольшую ширину и длину каждого листа и, используя коэффициент, находили площадь листа.

Пример. Длина листа Дл = 62 мм, а ширина по диагонали ромба Ш = 40 мм. Площадь ромба рассчитывают по формуле

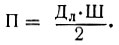
Для сорта яблони антоновка площадь ромба от общей площади листа составляет 69,5%, то есть коэффициент по методике М. К. Полякова равен 139. Определяем площадь целого листа:

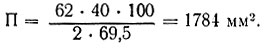
Таким образом, площадь листа равна произведению длины на ширину листа, деленному на коэффициент.

Полученные данные на I опытном участке показали, что самая большая площадь (36,47 см2) и вес (1,08 г) листа в 1964 г. были при расстоянии между дренами 24 м и глубине осушения 1,0 м (табл. 21 и 22).

Для установления прироста диаметра ствола С. С. Рубин (1967) измерял толщину ствола на всех учетных деревьях в трех местах: в середине, на расстоянии 1/4 и 3/4 высоты от земли. Во всех вариантах опыта наибольшее утолщение ствола наблюдалось в нижней части и наименьшее - в верхней. Но вполне возможно ограничиться обмером посредине ствола, поскольку эти данные совершенно тождественны средним, выведенным из трех измерений. Также следует отметить, что наиболее четкую картину по учету утолщения ствола дает вычисление площади поперечного сечения.

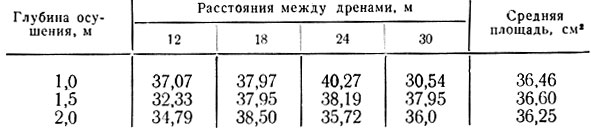
Таблица 21. Площадь одного листа, см2

Таблица 22. Вес листа, г

По данным С. С. Рубина (1967), сильные темпы прироста ствола продолжаются от посадки до 20-летнего возраста, затем ослабевают (рис. 38).

Наши многолетние данные по приросту ствола на I и II опытных участках были обработаны методом математической статистики по составленной программе.

На I опытном участке ежегодный прирост ствола за 1963-1969 гг. составил 9,5 мм и подчиняется прямолинейной зависимости

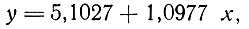
где у - ежегодный прирост диаметра ствола, мм;

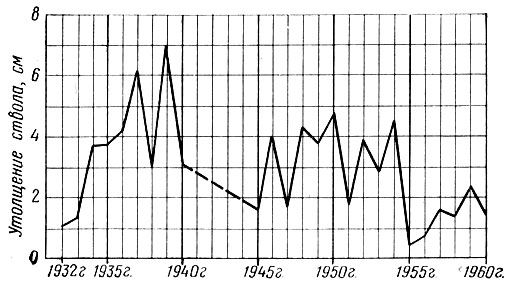
Рис. 38. Утолщение ствола яблони сорта Пепинка литовская (по данным С. С. Рубина)

Для этой зависимости коэффициент корреляции r=0,759 и число наблюдений n = 249.

В наших условиях сады были посажены в 1959 г., а в 1963 г. начаты исследования, поэтому для 1963 г. Х= 1, для 1964 г. х = 2 и так далее.

Из вышеуказанного уравнения получаем, что в 1963 г. средний прирост диаметра ствола составил 6,20 мм, а в 1969 г.- 12,79 мм.

Для определения прироста диаметра ствола в зависимости от глубины осушения и расстояния между дренами составлены уравнения по данным I опытного участка за 1963-1969 гг. (табл. 23).

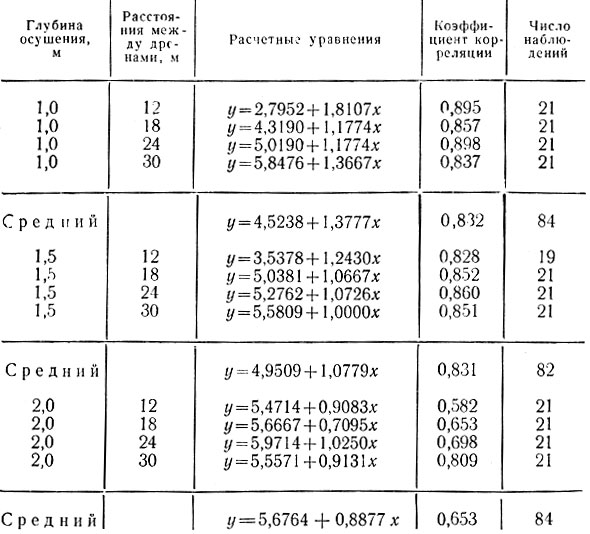
Таблица 23. Уравнения для определения ежегодного прироста диаметра ствола

Следует отметить, что при определении среднего арифметического с тремя повторностями для каждого варианта осушения выделялось три ряда плодовых деревьев. Таким образом, за семь лет число наблюдений составило 21. Анализ прямолинейных зависимостей при разных глубинах осушения и принятом среднем расстоянии между дренами показывает, что самый интенсивный прирост диаметра ствола происходит на участке, осушенном дренажем глубиной t= 1,0 м, а самый медленный - при глубине осушения t = 2,0 м (рис. 39, а).

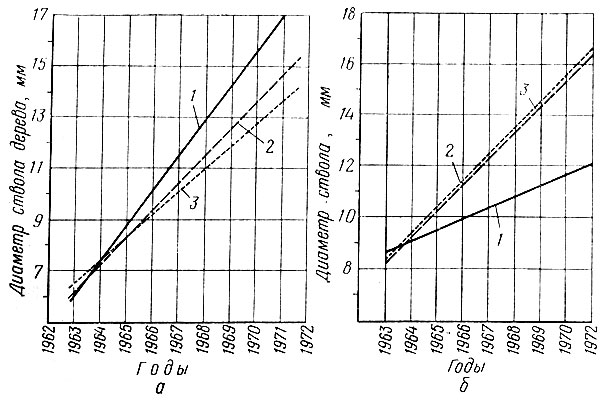
Рис. 39. Прирост диаметра ствола при разных глубинах осушения: а - на I опытном участке; 1, 2, 3 - глубина заложения дрен соответственно 1,0; 1,5; 2,0 м; б - на II опытном участке; 1, 2, 3 - глубина заложения дрен соответственно 0,7 1,1; 1,5 м

На II опытном участке в течение 1963-1971 гг. прирост диаметра ствола, средний для всех вариантов осушения, выражается следующим уравнением:

Коэффициент корреляции r = 0,417, число наблюдений n = 241.

Таким образом, в 1963 г. прирост диаметра ствола составил y1 = 7,18 мм, а в 1971 г. y9 = 13,51 мм, то есть увеличился на 87%.

Сравнение полученных данных при разных глубинах осушения (0,7; 1,1; 1,5 м) показывают, что наименьший прирост диаметра ствола получается при t = 0,7 м (рис. 39,б).

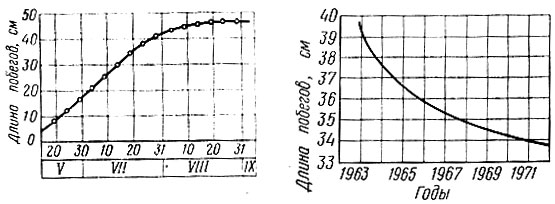
Рис. 40. Прирост побегов на I опытном участке при глубине осушения 1,5 м: а - за вегетационный период; б - за период с 1963 по 1971 г.

Процентный прирост диаметра ствола выражается следующим уравнением:

Корреляционный коэффициент r = 0,7, число наблюдений n=243.

Следует отметить, что в 1963 г. прирост ствола составил 27,34% общего диаметра, а в 1971 г. только 10,91%.

Для определения средней длины однолетнего побега каждый год в конце вегетационого периода на изучаемых деревьях подсчитывают суммарную длину и число побегов. В последние годы, когда деревья стали большими, прирост побегов измеряли только на определенных ветках.

С. С. Рубин (1967) указывает, что средняя длина побега значительно меньше реагирует на изменение условий роста деревьев, чем суммарный прирост всех побегов на дереве.

Учитывая, что в течение вегетационного периода рост побегов происходит с неодинаковой интенсивностью, автором был проведен следующий опыт. В 1965 г. начиная с весны через каждые пять дней измерялся рост побегов на десяти плодовых деревьях. Полученные данные показали, что самый интенсивный рост побегов происходит в первой половине лета и достигает 9 мм в сутки (рис. 40, а).

По данным С. С. Рубина (1967), средняя длина однолетнего побега при систематической обработке почвы в междурядье изменяются в широких пределах - от 11,0 до 34,3 см.

V. Venskutonis (1959) указывает, что на вегетативный рост яблонь отрицательное влияние оказывает недостаток влаги, проявившийся в фазе интенсивного вегетационного роста.

Годовой количественный прирост и суммарная длина побегов яблонь с периодическим плодоношением значительно колеблется. В неурожайные годы количество побегов уменьшается.

На I опытном участке при обработке данных за период с 1963 по 1971 г. по методу математической статистики получили резкую периодичность роста побегов, а общий вид изображен на рисунке 40, б.

При многолетних данных средняя длина побега может быть определена по уравнению

Несмотря на большое число данных n = 249, все-таки коэффициент корреляции получился небольшой - r = 0,233.

Пользуясь данным уравнением, получаем, что в 1968 г. средняя длина побега была 39,38 см, а в 1969 г. только 34,66 см, что в среднем составляет 36,37 см.

Исходя из данных исследований получаем, что длина прироста побега имеет тенденцию уменьшаться и подчиняется общей зависимости

На II опытном участке среднюю многолетнюю длину побега можно выразить следующим уравнением:

Для этого уравнения коэффициент корреляции r = 0,732, а число опытов n = 216.

Средняя величина побега на II опытном участке составляет 36,56 см, а с 1963 г. по 1971 г. она уменьшилась от 50,91 до 27,67 см.

Следует отметить, что как на I, так и на II опытном участке средняя длина побега составляла 36,5 см.

Таким образом, прирост диаметра ствола плодовых деревьев с каждым годом увеличивается и подчиняется прямолинейной зависимости, а длина побегов уменьшается и имеет вид логарифмической кривой.